 Sur les géométries non euclidiennes
Sur les géométries non euclidiennes
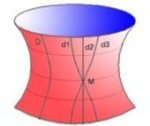
Exemple de géométrie hyperbolique.
« Dans le refus de reconnaître un statut mathématique aux géométries non euclidiennes, ce n’était pas seulement la vérité mathématique de la géométrie euclidienne qui était en jeu, mais son hégémonie, comme seule géométrie véritable possible ; et derrière l’enjeu épistémologique - défendre la primauté d’une théorie scientifique -, se profilait un enjeu ontologique, symbolisé par le statut du Vème postulat appréhendé d’abord comme une vérité physique avant d’être pensé dans son rôle logique de principe de démonstration. »
Extrait du livre Sur les géométries non euclidiennes / Documents pour travaux interdisciplinaires philo-math, éditeur IREM de Poitiers, juin 1995, de D. Gaud - J. Guichard - J.P. Sicre et J. Souville.
« Ne sachant pas le démontrer, Euclide admit le résultat suivant (cinquième postulat d’Euclide) : "Un point A et une droite D étant donnés, il passe par A une et une seule droite parallèle à D." En géométrie plane, ce résultat semble évident.
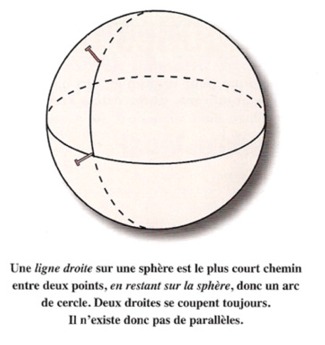
Mais plaçons-nous sur une sphère. Le plus court chemin entre deux points est obtenu en suivant l’arc de grand cercle entre eux. Sur une sphère, deux grands cercles se coupent toujours. Autrement dit, deux droites ne sont jamais parallèles ! Le cinquième postulat d’Euclide y est faux.
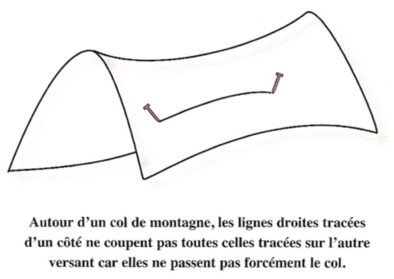
Si nous nous plaçons sur une surface différente comme un col de montagne, par un point il peut passer plusieurs parallèles à une droite donnée. Autour d’un col de montagne, les lignes droites tracées d’un côté ne coupent pas toutes celles tracées sur l’autre versant car elles ne passent pas forcément le col.
Nous avons donc plusieurs modèles de "plans" vérifiant tous les axiomes d’Euclide, à l’exception du fameux cinquième postulat. Dans certains modèles, celui-ci est vrai, et dans d’autres, il est faux. »
Extrait de l’article d’Hervé Lehning, « La logique, entre quotidien, mathématiques et philosophie », publié dans Tangente Hors-série n°38 - Mathématiques et philosophie, Éditions POLE, Paris 2010, p. 51.

